When inductors are connected in series or parallel, their equivalent inductance changes depending on the connection, similar to resistors.

1. Inductors in Series

For inductors in series, the total or equivalent inductance L_eq​ is simply the sum of all individual inductances. This is because the magnetic fields of each inductor add up, increasing the overall inductance.

                                                              L_eq = L₁ + L₂ + L₃+…. L_n

Example 1:

If two inductors with inductances of 𝐿₁=2H and 𝐿₂=3H are connected in series. The total inductance in series is 𝐿_eq = 2+3 = 5H.

2. Inductors in Parallel

For inductors in parallel, the equivalent inductance L_eq​ is calculated using the reciprocal of the sum of the reciprocals of each inductance.

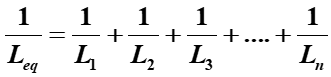
or

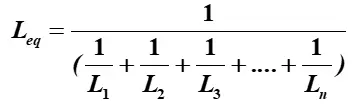
Example 2:

If two inductors with inductances of 𝐿₁=2H and 𝐿₂=3H are connected in parallel. The total inductance in parallel is

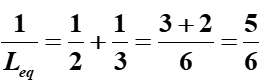
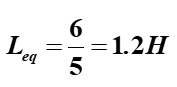
Few numerical problems involving inductors in series and parallel configurations

Problem 1: Inductors in Series

Three inductors with values 𝐿₁=2 H, 𝐿₂=4 H, and 𝐿₃=6 H are connected in series. Calculate the total inductance.

Solution:

For inductors in series, the total inductance is the sum of individual inductances.

                                                            L_eq = L₁ + L₂ + L₃
Substitute the values:

                                                            L_eq = 2+4+6=12H

Answer: The total inductance is 12 H.

Problem 2: Inductors in Parallel

Two inductors with values 𝐿₁=3 H and 𝐿₂=6 H are connected in parallel. Find the total equivalent inductance.

Solution:

For inductors in parallel, the total inductance is given by:

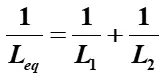
Substitute the values:

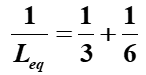
Finding a common denominator:

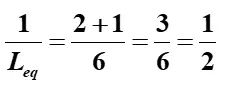
Thus,

                                                          L_eq = 2

Answer: The total inductance is 2 H.

Problem 3: Combination of Series and Parallel Inductors

Three inductors with values 𝐿₁=2 H​, 𝐿₂=4H, and 𝐿₃=8 H are connected as follows:

• • L₁ and 𝐿₂ are connected in series.
  • The series combination of L₁ and L₂ is connected in parallel with L₃​.

Calculate the total equivalent inductance of the network.

Solution:

Step 1: Calculate the series combination of L₁​ and L₂​.

                                                          L_Series = L₁ + L₃ = 2+4 = 6H

Step 2: Now, the series combination L_series = 6 H is in parallel with L₃=8 H.

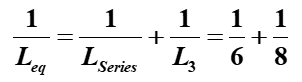
Find a common denominator:

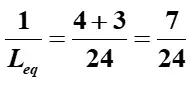
Therefore,

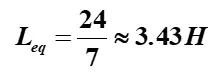
Answer: The total equivalent inductance is approximately 3.43 H.

Problem 4: Series and Parallel Combination with Three Inductors

You have three inductors: L₁=1 H, L₂=3 H and L₃=6 H.

• L₁​ and L₂ are connected in parallel, and this combination is connected in series with L₃​.

Calculate the total inductance.

Solution:

Step 1: Calculate the parallel combination of L₁​ and L₂​.

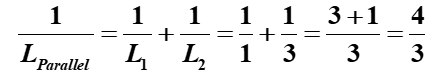
So,

Step 2: The parallel combination L_Parallel =0.75 H is in series with L₃ = 6 H.

                                                        L_eq = L_Parallel + L₃ = 0.75 + 6 = 6.75 H
 

Answer: The total inductance is 6.75 H.