Digital Electronics: Classification & Basic Terminologies
Digital Electronics is a branch of electronics that deals with circuits and systems that operate using digital signals. Digital electronics work with discrete signals (typically binary: 0 and 1). These binary signals represent two distinct voltage levels, such as:
- 0 (Low Voltage): Represents “false” or “Off.”
- 1 (High Voltage): Represents “true” or “On.”
Digital electronics form the foundation of modern computing, communication, and control systems. They are used to design and implement devices that perform logical operations, arithmetic calculations, data storage, and signal processing.
Classification of Digital Circuits
Digital circuits are primarily classified into Combinational Circuits and Sequential Circuits, based on their functionality and behavior.
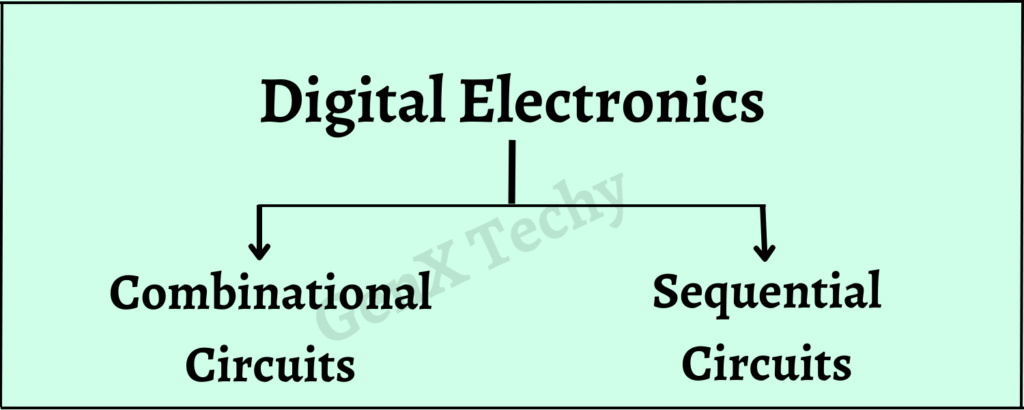
Fig. 1: Classification of Digital Electronics
1. Combinational Circuits: (Output depends only on present inputs)
A combinational circuit is a type of digital circuit where the output depends only on the current input and not on any previous inputs or states. In other words, combinational circuits do not have memory elements, and their output is solely determined by the combination of input values at any given time.
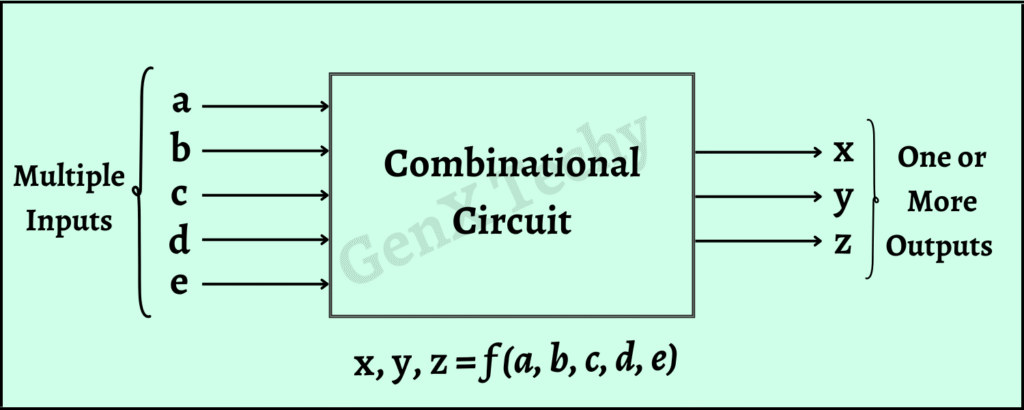
Fig. 2: Block Diagram of Combinational Circuit
Mathematical Representation
Combinational Circuit output is a function of the current input:
x, y, z = f(a, b, c, d, e)
Key Characteristics of Combinational Circuits
a) No Memory:
Combinational circuits do not store any past input or state information. They lack memory elements like flip-flops or registers.
b) Output Depends on Current Input:
The output is a direct function of the present input values. If the input changes, the output will change immediately (after a small propagation delay).
c) Fast Operation:
Since there is no feedback or memory, combinational circuits operate quickly.
d) Built from Logic Gates:
Combinational circuits are constructed using basic logic gates such as AND, OR, NOT, NAND, NOR, XOR, and XNOR.
e) No Clock Signal:
Combinational circuits do not require a clock signal for operation, unlike sequential circuits.
2. Sequential Circuits: (Output depends on present and past inputs)
- A sequential circuit is a type of digital circuit where the output depends not only on the current input but also on the sequence of past inputs.
- Sequential circuits have memory elements (e.g., flip-flops, registers) that store information about previous states, making them capable of retaining and using historical data.
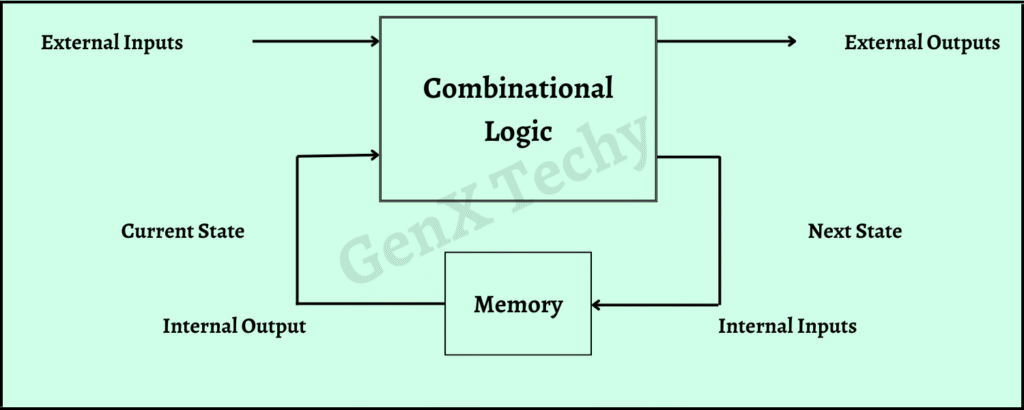
Fig. 3: Block Diagram of Sequential Circuit
Mathematical Representation
- Sequential circuit output depends on the current input and the current state:
Y(t) = g(S(t), X(t))
Where,
Y(t): Current output.
g: Output function.
- Next state depends on the current state and input:
S(t+1) = f(S(t), X(t))
Where,
S(t+1): Next state.
S(t): Current state.
X(t): Current input.
f: Transition function.
Key Characteristics of Sequential Circuits
a) Memory Elements:
Sequential circuits include memory elements like flip-flops or latches to store past states.
b) Output Depends on Current Input and Past States:
The output is a function of both the current input and the previous state(s) stored in memory.
c) Feedback Path:
Sequential circuits often have feedback paths that allow the output to influence future states.
d) Clock Signal:
Most sequential circuits are synchronized using a clock signal, which controls the timing of state transitions.
e) Stateful Operation:
Sequential circuits operate based on a finite number of states, making them suitable for tasks requiring memory or sequence detection.
Differentiate between Combinational Circuits and Sequential Circuits
| Feature | Combinational Circuits | Sequential Circuits |
|---|---|---|
| Output Dependency | Depends only on current input. | Depends on current input and past states. |
| Memory Elements | No memory elements. | Contains memory elements (e.g., flip-flops). |
| Feedback | No feedback paths. | Feedback paths are present. |
| Clock Signal | No clock signal required. | Clock signal is often used. |
| Complexity | Simpler design. | More complex design. |
| Speed | Faster operation. | Slower operation. |
| Examples | Adders, Multiplexers, Decoders. | Counters, Shift Registers, FSMs. |
| Applications | Arithmetic, data routing, code conversion. | Memory, control systems, sequence detection. |
