Data Structure: Multi-Dimensional Array

We are going to explore multi-dimensional arrays in C. Think of these as “arrays of arrays” that help store data in a structured way, like tables or matrices. If you’ve worked with 1D arrays (simple lists), this is the next step!But question arises, why do we need multi-dimensional arrays?Imagine storing marks of students in different subjects, or representing a chessboard (8×8 grid)—a single list (1D array) won’t be enough. We need rows and columns, and that’s where 2D, 3D, or higher-dimensional arrays come in!

What is an Array? (Quick Recap)

Before understanding multi-dimensional arrays, let’s first understand what a one-dimensional (1D) array is.

An array is like a container or a list that holds multiple values of the same data type (like all integers or all characters).
The position of each item in the array is called an index.

Example of a 1D array:

Example of a 1D array:
int numbers[5] = {10, 20, 30, 40, 50};
This is just like:
Index:01234
Value:1020304050

Multi-Dimensional Array

A multi-dimensional array is an array that contains one or more arrays as its elements. While a single-dimensional (1D) array represents a linear list of elements, multi-dimensional arrays allow you to store data in a structured tabular format (like rows and columns) or even higher-dimensional structures.

Types of Multi-Dimensional Arrays:

a) 2D Arrays (Matrix) → Stores data in rows and columns (like a table).

b) 3D Arrays → Can be visualized as a collection of tables (like a cube).

c) N-Dimensional Arrays → Higher-dimensional structures (rarely used beyond 3D).

Two-Dimensional (2D) Arrays in C

A 2D array (two-dimensional array) is an array of arrays that stores data in a row-column format, similar to a table or grid. It is useful when you need to represent structured data like:

Matrices in mathematics
Game boards (chess, tic-tac-toe)
Pixel data in images
Spreadsheets or tabular data

2D Array Structure (3×3 Example)

A 2D array is like a table with rows and columns as shown in figure below:
Position of elements in a 2D array is designated as arr[Row][Col]
Indexing starts from Zero. Row and column indices always start at 0.
arr[0][0] is the first element.
arr[i][j] refers to the element in the i-th row and j-th column.

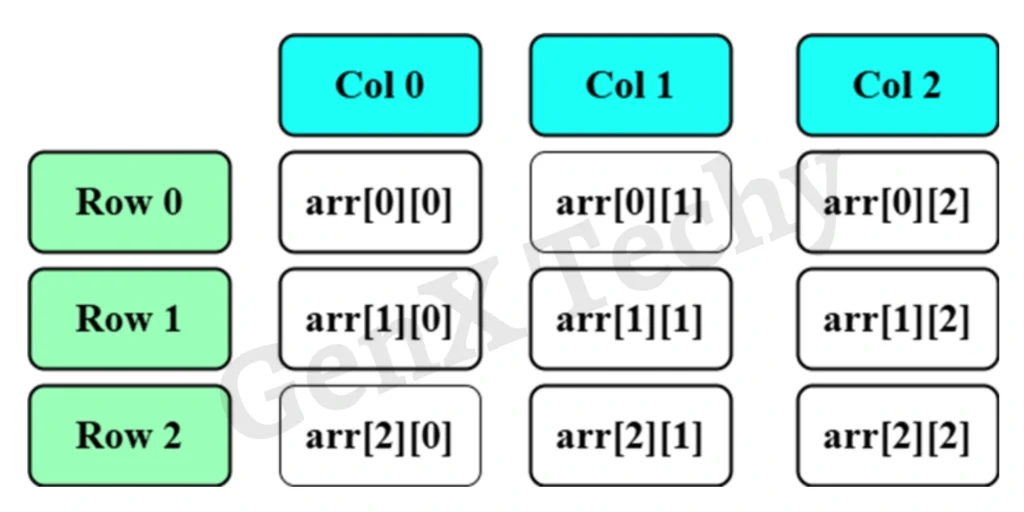
Fig: Position of elements in a 2D array

Declaration & Initialization

Syntax:

data_type array_name[rows][columns];

Different types of element initialization in a 2D array matrix

1) Static Initialization

int matrix[2][3] = {
    {1, 2, 3}, // Row 0
    {4, 5, 6}  // Row 1
};

2) Partial Initialization (Unfilled elements = 0)

int grid[3][3] = {
    {1, 2},       // Row 0: 1, 2, 0
    {4},          // Row 1: 4, 0, 0
    {7, 8, 9}     // Row 2: 7, 8, 9
};

3) Dynamic Input (User Input)

int rows = 2, cols = 3;
int arr[rows][cols];

for (int i = 0; i < rows; i++) {
    for (int j = 0; j < cols; j++) {
        printf("Enter arr[%d][%d]: ", i, j);
        scanf("%d", &arr[i][j]);
    }
}

Basic 2D Array (Matrix) Examples

Example 1: Store and print a 3×3 matrix

#include <stdio.h>

int main() {
    int matrix[3][3] = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}
    };

    // Print the matrix
    printf("Matrix:\n");
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            printf("%d ", matrix[i][j]);
        }
        printf("\n"); // New line after each row
    }

    return 0;
}

Output:

Matrix:

1 2 3
4 5 6
7 8 9

Example 2: Sum of Two Matrices (Add two 2×2 matrices)

#include <stdio.h>

int main() {
    int A[2][2] = {{1, 2}, {3, 4}};
    int B[2][2] = {{5, 6}, {7, 8}};
    int sum[2][2];

    // Compute sum
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            sum[i][j] = A[i][j] + B[i][j];
        }
    }

    // Print result
    printf("Sum of A and B:\n");
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            printf("%d ", sum[i][j]);
        }
        printf("\n");
    }

    return 0;
}

Output:

Sum of A and B:
6 8
10 12

Example 3: Transpose a Matrix (Swap rows and columns of a 3×2 matrix.)

int main() {
    int mat[3][2] = {{1, 2}, {3, 4}, {5, 6}};
    int transpose[2][3];

    // Compute transpose
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 2; j++) {
            transpose[j][i] = mat[i][j];
        }
    }

    // Print transpose
    printf("Transpose:\n");
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 3; j++) {
            printf("%d ", transpose[i][j]);
        }
        printf("\n");
    }

    return 0;
}

Output:

Transpose:
1 3 5
2 4 6

Index:	0	1	2	3	4
Value:	10	20	30	40	50