Data Structure: Multi-Dimensional Array
What is an Array? (Quick Recap)
Before understanding multi-dimensional arrays, let’s first understand what a one-dimensional (1D) array is.- An array is like a container or a list that holds multiple values of the same data type (like all integers or all characters).
- The position of each item in the array is called an index.
Example of a 1D array:
This is just like:
| Index: | 0 | 1 | 2 | 3 | 4 |
| Value: | 10 | 20 | 30 | 40 | 50 |
Multi-Dimensional Array
A multi-dimensional array is an array that contains one or more arrays as its elements. While a single-dimensional (1D) array represents a linear list of elements, multi-dimensional arrays allow you to store data in a structured tabular format (like rows and columns) or even higher-dimensional structures.Types of Multi-Dimensional Arrays:
a) 2D Arrays (Matrix) → Stores data in rows and columns (like a table).
b) 3D Arrays → Can be visualized as a collection of tables (like a cube).
c) N-Dimensional Arrays → Higher-dimensional structures (rarely used beyond 3D).
Two-Dimensional (2D) Arrays in CA 2D array (two-dimensional array) is an array of arrays that stores data in a row-column format, similar to a table or grid. It is useful when you need to represent structured data like:
- Matrices in mathematics
- Game boards (chess, tic-tac-toe)
- Pixel data in images
- Spreadsheets or tabular data
2D Array Structure (3×3 Example)
- A 2D array is like a table with rows and columns as shown in figure below:
- Position of elements in a 2D array is designated as arr[Row][Col]
- Indexing starts from Zero. Row and column indices always start at 0.
- arr[0][0] is the first element.
- arr[i][j] refers to the element in the i-th row and j-th column.
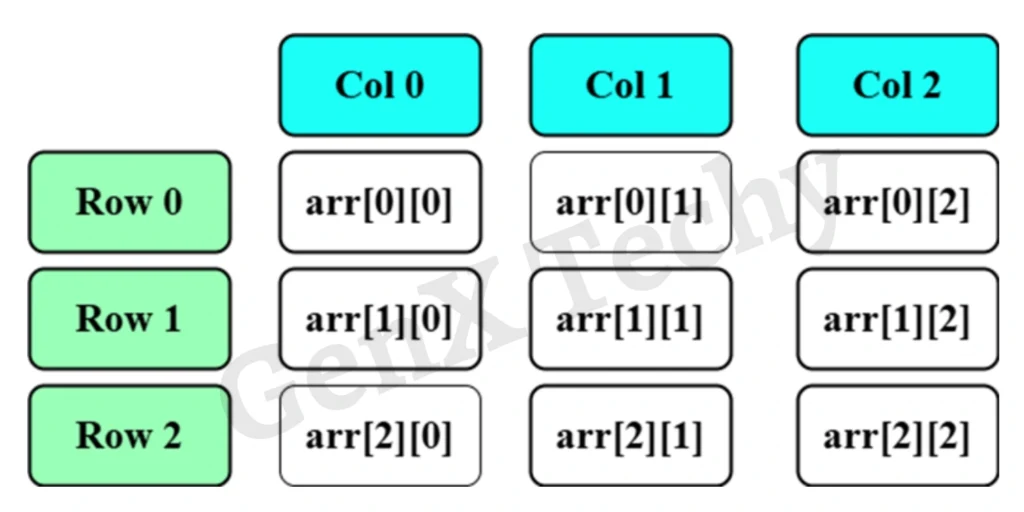
Fig: Position of elements in a 2D array
Declaration & Initialization
- Syntax:
- Different types of element initialization in a 2D array matrix
int matrix[2][3] = {
{1, 2, 3}, // Row 0
{4, 5, 6} // Row 1
};
2) Partial Initialization (Unfilled elements = 0)
int grid[3][3] = {
{1, 2}, // Row 0: 1, 2, 0
{4}, // Row 1: 4, 0, 0
{7, 8, 9} // Row 2: 7, 8, 9
};
int rows = 2, cols = 3;
int arr[rows][cols];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
printf("Enter arr[%d][%d]: ", i, j);
scanf("%d", &arr[i][j]);
}
}
Basic 2D Array (Matrix) Examples
Example 1: Store and print a 3×3 matrix
#include <stdio.h>
int main() {
int matrix[3][3] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
// Print the matrix
printf("Matrix:\n");
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
printf("%d ", matrix[i][j]);
}
printf("\n"); // New line after each row
}
return 0;
}
Output:
Matrix: 1 2 3 4 5 6 7 8 9
Example 2: Sum of Two Matrices (Add two 2×2 matrices)
#include <stdio.h>
int main() {
int A[2][2] = {{1, 2}, {3, 4}};
int B[2][2] = {{5, 6}, {7, 8}};
int sum[2][2];
// Compute sum
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
sum[i][j] = A[i][j] + B[i][j];
}
}
// Print result
printf("Sum of A and B:\n");
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
printf("%d ", sum[i][j]);
}
printf("\n");
}
return 0;
}
Output:
Sum of A and B: 6 8 10 12
Example 3: Transpose a Matrix (Swap rows and columns of a 3×2 matrix.)
int main() {
int mat[3][2] = {{1, 2}, {3, 4}, {5, 6}};
int transpose[2][3];
// Compute transpose
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 2; j++) {
transpose[j][i] = mat[i][j];
}
}
// Print transpose
printf("Transpose:\n");
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 3; j++) {
printf("%d ", transpose[i][j]);
}
printf("\n");
}
return 0;
}
Output:
Transpose:
1 3 5
2 4 6
