What is a Number System?

A number system is a mathematical framework used in the systematic representation, expression, and manipulation of numbers. It defines a set of symbols (digits) and rules for combining them to form meaningful numerical values. Different number systems use different bases (also called radices), which determine how many distinct digits are available in that system.

Key Components of a Number System

1. Base (Radix): The total number of unique digits (including zero) used in the system.

Example:

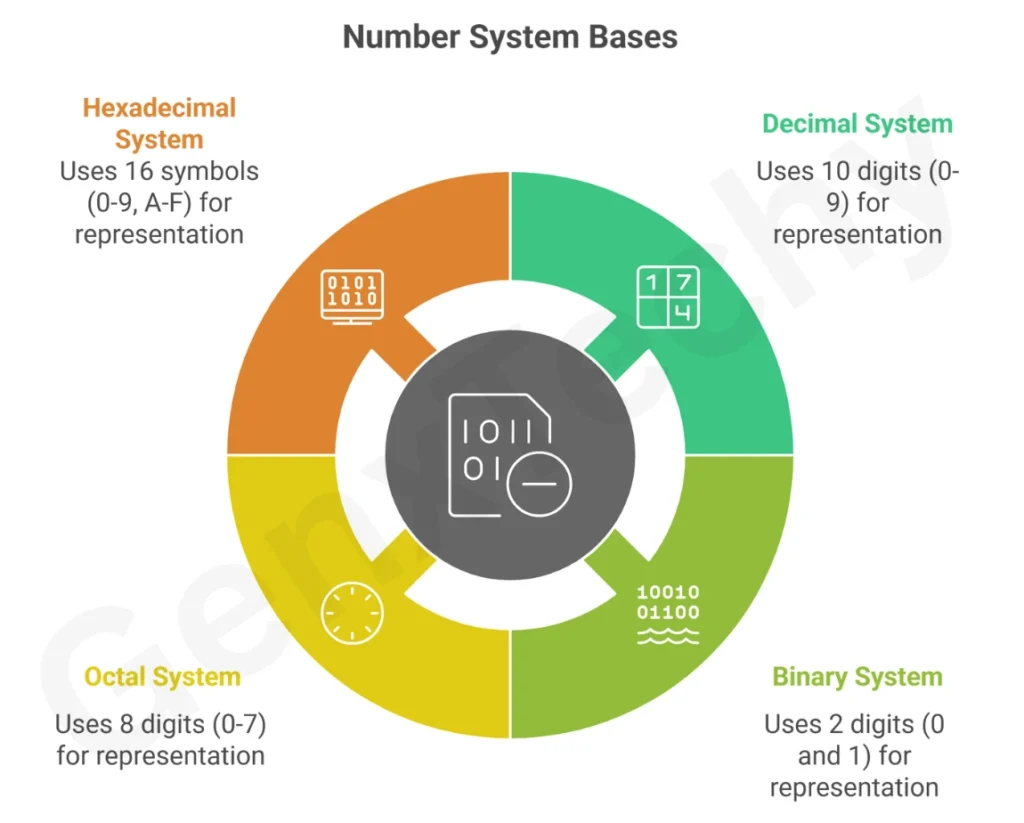
a) In Decimal (Base-10),the digits are 0 to 9.

b) In Binary (Base-2), the digits are 0 and 1.

c) In Octal (Base-8), the digits are 0 to 7

d) In Hexadecimal (Base-16),the digits are 0–9 and A–F.

2. Positional Value (Place Value): Each digit’s value depends on its position (place) in the number.

Example: In 253₁₀,

a) The number 2 is in the hundreds position (2 × 10² = 200).

b) The number 5 is in the tens position (5 × 10¹ = 50).

c) The number 3 is in the ones position (3 × 10⁰ = 3).

3. Digits (Symbols): The symbolic representation of numbers in the system.

Types of Number Systems

1) Decimal Number System (Base-10)

• Most commonly used in daily life.
• Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Example: The decimal number 45₁₀ may be simplified as (4 × 10¹ ) + (5 × 10^⁰) = 40 + 5 = 45.

2) Binary Number System (Base-2)

• Used in computers and digital systems.
• Digits: 0 and 1 (called bits).
• Example: The binary number 1011₂ means (1 × 2³) + (0 × 2²) + (1 × 2¹) + (1 × 2⁰) = 8 + 0 + 2 + 1 = 11₁₀.

3) Octal Number System (Base-8)

• Used for concise binary representation in computation.
• Digits: 0 to 7.
• Example: 34₈ means (3 × 8¹) + (4 × 8⁰) = 24 + 4 = 28₁₀.

4) Hexadecimal Number System (Base-16)

• Extensively used in memory addressing and programming.
• Digits: From 0 to 9 and from A to F, where A=10, B=11, C=12, D=13, E=14, F=15.
• Example: The Hexadecimal number 2F₁₆ means (2 × 16¹) + (15 × 16⁰) = 32 + 15 = 47₁₀.

Significance of Number Systems

Number systems are foundational to mathematics, technology, and daily life. Their significance extends far beyond simple counting, influencing everything from basic arithmetic to the functioning of modern computers and secure identification systems.

1) Unique Representation and Mathematical Structure

A number system is a consistent way of expressing numbers using digits or symbols. It offers a distinctive representation for each number, which is indicative of the arithmetic and algebraic structure of the figures. This enables us to execute operations such as addition, subtraction, multiplication, and division with precision and efficiency.

2) Essential for Counting, Measuring, and Labeling 

Numbers, as represented within a number system, are essential for counting objects, measuring quantities, and labeling items. Without a standardized system, it would be impossible to consistently record or communicate quantities, dates, time, money, or measurements in any field.

3) Identification, Ordering, and Tallying

Number systems serve three fundamental purposes in society:

• • Identification: Numbers are used to uniquely identify people (e.g., social security numbers), products (e.g., serial numbers), and accounts (e.g., bank account numbers), enhancing security and minimizing confusion.
  • Ordering: Numbers define order in sequences, such as ranking in sports or arranging data, using ordinal numbers (first, second, third, etc.).
  • Tallying: Numbers allow us to total or count items, essential for inventory, statistics, and resource management.

4) Foundation of Digital Technology

Modern digital systems, including computers and electronic devices, rely on specific number systems—primarily binary and hexadecimal. Programming, digital electronics, and computer science need understanding these systems. Hexadecimal (base-16) is utilized in programming and data representation, whereas binary (base-2) underlies all digital data processing.

5) Efficient Data Representation & Storage

Hexadecimal (Base-16) and Octal (Base-8) make binary data easier to understand:

• • Long binary strings (e.g., 110110101011) are cumbersome; hex (DAB) is more compact.
  • Used in memory addressing, assembly language, and debugging.

Binary-Coded Decimal (BCD) ensures accurate decimal representation in digital clocks and calculators.

6) Enables Arithmetic & Logical Operations

Different number systems allow optimized calculations:

• • Binary arithmetic is used in ALU (Arithmetic Logic Unit) operations.
  • Floating-point representation (IEEE 754) uses binary exponents for scientific computing.

Boolean algebra (AND, OR, NOT) relies on binary logic.

7) Supports Multiple Computing Applications

Programming & Data Encoding:

• • Hex is used in color codes (e.g., #FF5733), Unicode, and MAC addresses.
  • ASCII/Unicode rely on binary to represent text characters.

Networking & Cryptography:

• • IP addresses (IPv4 in decimal-dot notation, IPv6 in hexadecimal).
  • Encryption algorithms (RSA, AES) use binary operations.

8) Universal Communication and Standardization

A standardized number system allows for universal communication of quantities and values across languages and cultures. This standardization is vital for trade, science, education, and international collaboration.

9) Practical Applications in Daily Life

Number systems are ubiquitous in daily life, from telling time and managing finances to navigating technology and organizing information. They are crucial for understanding and interacting with the increasingly digital world.

10) Historical and Cultural Development

Number systems have evolved alongside human civilization. Early societies used tally marks, pebbles, or notches to keep count, which gradually developed into more abstract and efficient numeral systems. The adoption of place-value systems, such as the Hindu-Arabic numerals, revolutionized mathematics and commerce by enabling easier calculation and record-keeping.